User:Autisticfroggy/The Last Lecture

Transcript of the last lecture I gave to the mentor team before my retirement. It covers the mathematical background and system of fusionv6 and its finer points. Certain sections have been redacted as they describe exploits.

Part 1 - The Kicked Rotor

Fusion's two primary components, plasma and carbon dioxide, do not have any linear relationships like the rest of the atmos reactions. Their relationship is not even quadratic, cuboid, or any regular function. Instead, they follow an angular relationship that is governed by a mathematical system known as a kicked rotor. To picture this system, imagine a single rod upon which two hammers are attached perpendicularly, now imagine that you have the two hammers spin. These two hammers are the rotors, one of which is represented by plasma, the other is represented by carbon dioxide. The angular position of the rotors, which we shall assume as anything between 0~360 degrees or 0 to 2pi radians, serves as the primary measurement of where the rotors are at any given point. It is possible in this theoretical non euclidean space to extend the total traversable field of rotation beyond 2pi radians, or even below it, but the key part here is that once the rotor hits the maximum point of traversal, it goes back to 0, forming a complete rotation. This is why the plasma and CO2 mole counts keep jumping all over the place when you do fusion and appear to have no linear or even causal relationship, they are spinning rotors whose angular position is scaled up according to the volume of the vessel. As for how fast the rotors spin, this is where the kicked part of the kicked rotor system enters the scene. The instability factor of the fusion reactor refers to how much of a kick the rotors get and directly increments or decrements the angular positions of the rotors. Specifically, it multiplies by the sine of the angular position of the CO2 rotor, which means it can change direction of spin at any given kick (for 2pi radian bounded systems, this usually means a negative kick at angular ranges of 1/2 pi radians to 3/2 pi radians, and positive at the rest). The CO2 rotor is irrelevant and has its own rotation, but does not factor into further fusion calculations.

Toroidal size graph over volume.

Part 2 - The Hypertoroid

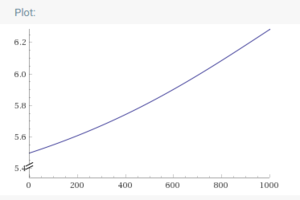
The hypertoroid is a representation of the entirety of fusion state space and has 4 dimensions, the angular position of the 2 rotors forming 2 dimensions, the maximum angular bound of the rotors forming the third (this variable is called the toroidal size and is static for most intents and purposes) and the instability which forms the fourth. All factors with the exception of the toroidal size wrap around once they hit their maximum point which is determined by the toroidal size. Toroidal size is determine by volume, as seen in the graph above, with 2pi radians being the value most commonly seen on standard 1000L canisters, with values going above 2pi radians (though not by much) as the volume increases. This means that you can theoretically cap the instability of a fusion reaction to 5 or so by using a small volume pipenet to hold your fusion reaction together, though I do not advise this. More importantly however, is that as different volumes produce different toroid sizes, they all have different optimal gas mixes. As such, a 2000L canister (as has been tried on tg) has a completely different optimum than your standard 1000L canister, and this must be taken into consideration when performing fusion in a large spaceloop. The second factor that must be taken into consideration aside from the rotors and the size is the toroidal scale. Fusion necessarily must scale down mole amounts into a space that can be bound between 0 and the toroidal size, to do this it stores a variable known as toroidal scale which also depends entirely on volume. This toroidal scale variable divides the mole amounts before angular positions are derived, then scales them back up afterwards to create the mole counts you are familiar with. This is highly abusable, but I will discuss that at a later point.

Chirikov Standard Map of the Kicked Rotor at K=1

Part 3 - Instability, Chaos and K-Parameters: A guide to reading Chirikov Standard Maps

Pictured above is the Chirikov standard map for a kicked rotor with a K parameter of 1. In fusion terms, that is the position of the plasma rotor across all of time if the instability remained at 1. The strobed orbits depicted represent parts of the torus state space where if the rotor was positioned, it would merrily orbit in a predictable fashion across time without interruption. Unfortunately for us, this assumes that the instability remains at 1 all the time, which is not possible due to emergent effects to be discussed in Part 4. Each color band represents a different possible orbit, with the white spaces representing chaotic positions where no stable orbit can be formed. It is possible to fine tune your fusion mix such that it is perfectly positioned to rotate at that axis, but doing so requires such precise control over gas inputs that it is functionally impossible. Instability is affected by the gasmix of the fusion reaction, with different gas types having different fusion power levels which are then all added together after being scaled by mole amount in the final gas mix to get a final fusion power total. This total is then constrained by the toroidal size to arrive at the final K parameter, or instability. Gases such as N2O increase instability, with nitryl having the highest fusion power, while pluoxium has a negative fusion power. In the end, the nature of the toroidal size constraint renders precise control useless, but does make it so that slight alterations to these gases end up resulting in an entirely different K parameter, which makes stable fusion orbits entirely unfeasible.

Part 4 - Energistics

As the fusion rotors spin, temperatures fluctuate wildly depending on the creation or destruction of mass. The fusion reaction generates a large amount of energy whenever plasma is destroyed, and consumes a large amount of energy when plasma is created. As the rotors spin, either creation or destruction is possible, but the reason why we start off with more plasma than carbon dioxide is because this places the starting rotor positions at one where plasma is likely to be destroyed, thus creating energy and hopefully enough of it to carry the rest of the reaction to completion. Here, energy creation and destruction are once again dependent on instability. If the instability falls below the endothermality threshold of 2, any energy lost to the creation of plasma is annulled and no change in temperature occurs. If the instability is in excess of 2 and plasma is created instead of destroyed, the amount of energy lost is scaled to an even higher amount. It is also important to note that due to heat capacity calculations, any drastic change in ratio of plasma to CO2 will magnify temperature changes despite the total thermal energy of the gasmix being the same. It is also very important to note that exothermic fusion reactions produce O2 and N2O scaled by how much energy was produced, and if the reaction was endothermic, it instead produces BZ and nitryl also scaled to how much energy was lost. This may seem trivial, but it is incredibly important to note as will become apparent in Part 5. I have also neglected to mention Tritium up until this point. This is because its only purpose is to be consumed in a linear fashion until it runs out. It serves as nothing more than a hard limit to prevent an eternally orbiting rotor system.

Part 5 - Knock-on effects and Chaos outside of the Kicked Rotor System

As noted in Part 4, fusion reactions produce excess gas byproducts. This has several, very important effects. First, the production of oxygen will trigger the standard combustion reactions of plasma and tritium. This is the single greatest cause of tritium shortages in fusion reactions. It also has the secondary effect of consuming plasma and producing CO2, lowering the amount of energy that a fusion reaction can produce by consuming the plasma. The N2O, while seeming trivial, has its own fusion power, which causes the K-parameter (instability) to change, invalidating any standard maps you plan on using and also making any hopes of a stable orbit impossible. The endothermic reactions also have their special knock-on effects. The production of nitryl and BZ, coupled with the production of N2O in the exothermic reaction and a steady plasma supply from the main rotor reaction creates all the necessary ingredients for the synthesis of stimulum, a highly valuable and profitable gas that is normally produced in small amounts due to the complexity of its quintic curve reaction. While this may result in only tiny gains, there are methods to exploit this design feature that will be discussed in part 6. There are other complexities that may interfere with your fusion reaction. Most setups generally involve heat exchanging a fusion can over a tritium burn chamber; wrenching your canister into the heat exchange net already causes your initial mix to be cut by a proportion due to sharing it with the heat exchange net, wrenching it back in the event your main can loses heat is also a valid method, but introduces external chaos. If doing open air fusion such as in the eclipse fusion engine, the gas shares between different turfs will also introduce new variables to account for, not that you needed more to track to begin with.

Part 6 - Exploits and side effects

<REDACTED BY ORDER OF MCOUNCIL>

Conclusion

There is too much chaos in fusionv6 to achieve stable orbits by the nature of the shifting k parameter and the byproducts, and even if they were removed the tritium hardcap would render it time constrained. The toroidal scale problem is so intrinsic to the design of fusion being so reliant on the single variable that is pipenet volume that it will be difficult to patch out without some clever mathematics, as such it will likely stay until fusionv7 will come out (currently under design by yours truly), or is hotfixed out by an emergency patch removing all fusion byproducts. I have not described how to fusion or even setups so this probably is insufficient for a wiki guide, but I'll deal with that later.

This will be my last atmos lecture for the foreseeable feature and will likely be my last one on yogs unless I decide to come back. It has been a pleasure serving with all of you and I wish you all the best. This is Colton Oppenheimer, signing out.